초·중·고 학생들을 위한
유클리드 원론

뒷 배경은 독서와 책에 대한 정조의 열정과 갈망이 담긴 10폭 평풍의 책가도(冊架圖)이다.
Euclid, «Euclid's Elements of Geometry. In XV. books», 1661, Printed, by R. & W. Leybourn, for Richard Tomlins. 속에 있는 유클리드에 색을 입힌 그림을 수정하였다.
초·중·고 학생들을 위한

전설에 의하면 위 구절은 플라톤이 세운 아카데미 입구 현판에 기록되었다고 한다. 이 전설은 엘리아스(Elias)처럼 아리스토텔레스의 몇몇 해설가들에 의해 전해졌는데, «ommentary on the Categories, XVIII, 118, 18-19»에는 "플라톤 아카데미에는, 뮤즈 신전이 있기 전에 다음과 같이 쓰여져 있었다. 기하학을 모르는 자는 이 문으로 들어오지 말아라.(In Plato's Academy, before the temple of the Muses was written: Let None But Geometers Enter Here)"와 같이 기록되어 있다. 그리고 존 필로포누스(John Philoponus)의 «Commentary on the soul, XV, 117.27»에서는 위 글의 단순한 버전으로 "기하학을 모르는 자는 이 문으로 들어오지 말아라.(Let None But Geometers Enter Here)"와 같이 수록되어 있다.
«Diogenes Laertius in IV»에는 플라톤의 가르침에서 기하학의 중요성을 보여 주는 다음과 같은 일화가 있다. 제노크라테스(Xenocrates)는 아카데미의 책임자였다. 그는 음악도, 기하학도, 천문학도 배우지 못했지만, 그래도 그의 강의를 듣고 싶어하는 사람에게, "당신은 철학에 의지할 것이 아무것도 없으므로, 당신의 길을 가세요."라고 말하였다. 또 다른 사람에게는 "당신이 양털을 깍으러 온 것은 나와 아무 상관이 없습니다"라고 말하였다고 한다. 철학을 모르면 아카데미에 들어 올 자격이 없다는 것으로 철학이 얼마나 중요한 과목 중 하나였음을 볼 수 있는 대목이다. 어딘가 비슷한 일화가 생각날 것이다. 유클리드와 그의 제자 사이의 일화이다. 유클리드에게서 기하학을 배우고 있던 제자가 스승에게 물었다. "선생님, 이토록 지겹고 쓸모가 없어 보이는 학문을 대체 뭣하러 가르치고 배우는 것입니까?" 유클리드가 노발대발하며 "배운 것에서 꼭 본전을 찾으려고 하는 놈에게 학문이 무슨 필요가 있겠느냐. 저 자에게 동전이나 몇 푼 던져주어 쫓아버려라."라는 일화이다.
그리고 «원론»과 연관된 유클리드 일화도 있다.
알렉산더 대왕(Alexander the Great)이 죽은 후 이집트의 첫 번째 왕인 프톨레미 소테르 1세(Ptolemy 1st Soter)는 개인적으로 유클리드를 후원하였다. 그러나 유클리드의 중요한 저서인 «원론»를 공부하기가 너무 어려워 유클리드에게 이 책을 통달할 수 있는 더 쉬운 방법을 알려달라고 하였다. 철학자 프로클루스(Proklos)에 의하면, 유클리드는 "폐하, 기하학에는 왕도가 없습니다.(Sire, there is no royal road to geometry.)"라고 유명한 농담을 했다고 한다. 주목할 점은 유클리드가 길을 의미하는 "odos(=road)"라는 단어를 사용하지 않고 지름길을 의미하는 "atrapos(=trail)"이라는 단어를 사용했다는 것이다.
 |
 |
 |
지금 이곳에 들어와 있는 여러분은 기하학을 알고 싶어할 것이다. 그러나 이미 기하학의 세계에 들어와 있다. 이제 유클리드 «원론»을 함께 연구하고 논의를 하였으면 한다.
유클리드 «원론» 원본 그대로 연구 및 학습하는 것은 매우 고통이 따른다. 일차적으로 용어 문제가 매우 크며, 대수적 표현으로는 간단히 나타낼 수 있는데 이를 그 당시의 사고로 생각을 한다는 것은 그리 쉬운 일은 아니다. 그래서 이곳에서는 초·중·고 학생들도 유클리드 «원론»을 직접 학습할 수 있도록 용어를 되도록 현 교육과정에 맞추어서 변환하려고 노력을 많이 기울였다. 그리고 유클리드 «원론» 유클리드 명제와 현대적 표현의 명제를 함께 서술하였다. 정의와 명제를 현대적 의미로 바꾸었으며 증명 자체도 수식으로 표현하여 가독성을 높였다. 그러나 유클리드 «원론» 증명 논리과정을 그대로 따라가려고 노력하였다. 증명도 중간에 뛰어 넘은 부분도 있어 증명의 삐진 부분을 채워 넣기도 하였다.
여기에 있는 유클리드 «원론»은 원본 그대로가 아니라는 점을 다시 한번 기억하자!
I 권은 정의 23개, 공리 5개, 일반 상식 5개, 명제 48개가 수록되어 있으며 '직선, 각, 삼각형'에 대한 내용으로 구성되어 있다. 필수적이고 예비적인 정의와 설명 및 공준과 공리로 시작한다. I 권의 명제 중에는 합동, 평행선, 직선으로 이루어진 도형 등에 관한 친숙한 명제들이 포함되어 있다. 특히 명제 47과 명제 48은 피타고라스 명제와 그 역에 대한 것이다.
평행선 공리와 동치 명제들은 많이 있다. 그 중에 몇가지에 대한 자료는 아래 링크 자료를 참고하시오.
II 권은 정의 2개, 명제 14개가 수록되어 있으며 '도형의 넓이'에 대한 내용으로 구성되어 있다. 겨우 14개의 명제만을 포함하고 있는 작은 책인데 여기에서는 주로 피타고라스 학파의 기하 대수학을 다루고 있다. 이 책의 명제 12와 명제 13은 근본적으로 오늘날 코사인 법칙으로 알려진 피타고라스 명제의 일반화이다.
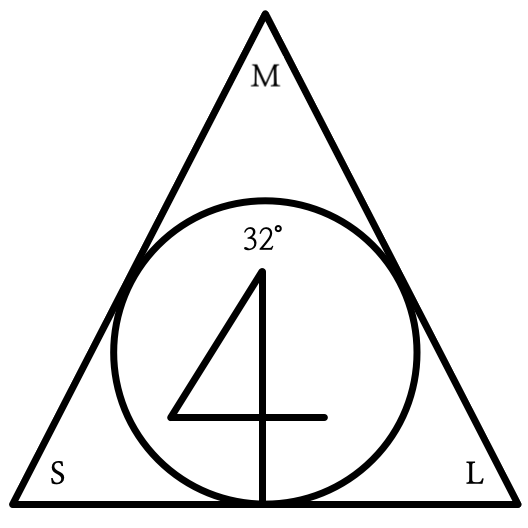
III 권은 정의 11개, 명제 37개가 수록되어 있으며 '원'에 대한 내용으로 구성되어 있다. 따름 명제 2개를 포함하여 39개의 명제로 이루어져 있고, 원, 현, 할선, 접선, 연관된 각도의 측정 등에 관한 명제들을 포함하고 있다.
IV 권은 정의 7개, 명제 16개가 수록되어 있으며 '다각형과 원'에 대한 내용으로 구성되어 있다. 자와 컴퍼스를 이용한 작도, 주어진 원에 내접하는 다각형 작도와 외접하는 다각형 작도, 정다각형 작도를 포함하고 있다.
V 권은 정의 18개, 명제 25개가 수록되어 있다. 비율 이론에 대한 대가 다운 설명을 하였다. 이 책은 수학적인 문헌 중에서 가장 훌륭한 걸작 중의 하나로 간주된다.
VI 권은 정의 4개, 명제 44개가 수록되어 있다. 이전 명제들을 닮음 도형의 연구에 응용하고 있다.
VII 권은 정의 22개, 명제 39개가 수록되어 있다. 두 개 이상의 정수에 대한 최대공약수를 구하는 방법(유클리드 호제법)으로 시작한다. 또한 초기 피타고라스 학파의 비율 이론에 대한 명제들을 발견할 수 있다.
VIII 권은 명제 27개가 수록되어 있다. 주로 연비례와 그것과 관련된 등비수열을 다루고 있다.
IX 권은 명제 36개가 수록되어 있다. 수론에서 중요한 많은 명제들이 있는데 먼저 명제 14는 중요한 ‘산술의 기본 정리(Fundamental theorem of arithmetic)’즉 “1 보다 큰 임의의 정수는 반드시 소수들의 곱으로 표현될 수 있으며 근본적으로 단 한가지 방법으로 표현된다.”는 명제와 동치이다. 명제 20에서 ‘소수의 개수는 무한하다.’는 명제에 대한 매우 세련된 증명을 찾아볼 수 있다. 명제 35는 등비수열의 첫 n개의 항의 합에 대한 공식을 기하학적으로 유도 했다. 그리고 이 책의 마지막 명제인 명제 36은 짝수인 완전수를 만드는 놀라운 공식을 증명하고 있다.
X 권은 정의 16개, 명제 115개가 수록되어 있다. 무리수, 즉 어떤 주어진 선분의 길이를 단위수(1)로 측정하여 비율로 나타낼 수 없는 길이를 다루고 있다.
XI 권은 정의 28개, 명제 39개가 수록되어 있다. 선과 면, 면과 면, 평행육면체, 정육면체, 각기둥들에 대한 명제들이 있다.
XII 권은 명제 18개가 수록되어 있다. 원의 넓이와 각뿔, 각기둥, 원뿔, 원기둥, 구의 부피(단, 원주율은 쓰지 않음.)등의 명제들이 있다. 원의 넓이는 지름의 제곱에 비례하고 구의 부피는 지름의 세제곱에 비례함을 이용하였다.
XIII 권은 명제 18개가 수록되어 있다. 정다면체는 다섯 종류 즉, 정사면체, 정육면체, 정팔면체, 정십이면체, 정이십면체 만이 있음을 증명하였다.
[1] David E. Joyce, https://mathcs.clarku.edu/~djoyce/java/elements/elements.html
[2] 이무현 역, 유클리드 저, «기하학 원론 가, 나, 다, 라», 2003, 교우사.
[3] Heath, «Thirteen Books of Euclid's Elements Vol 1, 2, 3», 1968, CAMBRIDGE.
[4] ROBERT MAYNARD HUTCHINS, «GREAT BOOKS OF THE WESTERN WORLD-Euclid_ Archimedes_ Apollonius of Perga_ Nicomachus of Gerasa - Euclid's Elements, works of Archimedes, On Conic Sections by Apollonius of Perga and Introduction-», 1952, William Benton.
[5] OLIVER BYRNE, «THE FIRST SIX BOOKS OF THE ELEMENTS OF EUCLID», 1847, LONDON WILLIAM PICKERING.
[6] JOHN CASEY, LL.D., F.R.S., «THE FIRST SIX BOOKS OF THE ELEMENTS OF EUCLID», 1885, DUBLIN: HODGES, FIGGIS, & CO., GRAFTON-ST. LONDON: LONGMANS, GREEN, & CO.
[7] Maureen T. Carroll and Elyn Rykken, «Geometry:The Line and the Circle», 2018, MAA PRESS, Vol 44.
◼ 황운구 ◼
⨳ 수학교육학 박사
⨳ 현 대전동신과학고등학교 교사
⨳ 이메일 :
![]()
⨳ 블로그 :
![]()
◼ 저서 ◼
⨳ «파스칼 삼각형», 토마스 M. 그린, 찰스 L. 햄버그 공저 · 황운구 , 전태환 , 서은원 , 최혜린 , 최수연 , 신석빈 공역,
지오북스, 2022년 1월
⨳ «택시 기하학», Eugene F. Krause 저 · 황운구, 권정인, 두은서, 이수연, 허민서 공역, 신한출판미디어, 2020년 8월
⨳ «종이접기 수학», 카즈오 하가 저 · 황운구 역 · 이대영 감수, 신한출판미디어, 2020년 3월
⨳ «수학 속 수수께끼», E. P. 노스롭 저 · 황운구 역, 수박스토리, 2020년 01월
⨳ «수학 속 패러독스», 황운구 저, 지오북스, 2019년 10월
⨳ «어떻게 비눗방울 안으로 들어갈까?», 알브리헤트 보이텔슈파허 저 · 황운구 서은원 최혜린 이호연 최수연 공역,
신한출판미디어, 2018년 8월
⨳ «사이클로이드», 황운구 저, 지오북스, 2017년 3월
⨳ «해시계», 황운구, 홍성일, 김지영 공저, 과학정원, 2015년 9월
⨳ «수학에서의 Flash 활용», 김향숙, 정인철, 박용운, 황운구 공저, 경문사, 2005년 1월
오타 및 오류가 있으면 그 내용을 이메일로 보내 주시면 검토 후 수정 및 업로드 하겠습니다.
유클리드 «원론» 작업은 처음 2015년 2월 경 부터 김*림, 유*수, 김*진, 류*우, 이*범, 권*율, 이*영, 최*린, 주*은, 양*현, 최*식 선생님들과 함께 연구를 시작하였다. I 권부터 IV 권까지 1차 연구, XI 권부터 XIII 권까지 2차 연구에서 한글과 지오지브라 애플릿 개발을 마무리를 하였으나 이후 연구의 어려움이 있어 연구가 중단되었다. 그 후 개인적으로 연구를 계속하여 유클리드 «원론»을 I권부터 명제와 정의를 지오지브라 애플릿과 HTML5로 작업을 하여 웹 서비스를 시작하였다. 위 선생님들의 노고가 없었더라면 지금에 이르기가 어려웠을 것이다. 위 선생님들께 고마운 마음과 감사의 말을 전한다. 또한 위 선생님들께 연구를 함께 마무리를 짖지 못하여 죄송스런 마음을 항상 가지고 있다.
중단 이후 저 혼자 다시 연구를 하였는데 용어와 증명 과정에 대한 어려움으로 두 번이나 연구를 멈추었다. 다시 마음을 다 잡고 2019년에 세 번째 도전을 하였다. 2023년 11월 까지 연구를 하여 13권 전체를 웹 서비스를 하고 있다.
부연설명에 대수적 증명, 다양한 질문들, 다른 기하학적 증명 등 부가적인 내용도 추가하고 있고, 정의, 명제, 증명의 검증 및 오류 수정도 함께 하고 있다. 나아가 '3Blue1Brown' 유튜브 체널에서 재공하는 영상들을 만드는 파이썬 라이브러리 매님(manim)으로도 시각화 증명도 작업을 하고 있다. 처음 개발 시 홈페이지 기본틀을 bootstrap 4.x로 개발을 하였으나 중간에 VII 권 부터는 bootstrap 5.x로 작업을 하고 있고 수정 작업에서 다시 bootstrap 5.x로 바꾸어 나아가고 있다. 그리고 용어도 같은 뜻이지만 중간에 또 바꾼 것도 있어서 통일되지 않은 점을 양해 바란다. 이러한 것도 수정 작업을 할 때 통일시켜 완벽을 기하도록 하겠다.
앞으로의 계획은 유클리드 «원론»을 다시 점검 및 수정 그리고 내용을 추가하는 것이다. 그리고 아폴로니우스 «이차곡선», 아르키메데스 «구와 원기둥»에 대하여 이와 같이 웹 서비스를 하려고 계획하고 있다.
마지막으로 이 서비스를 허락해주고 서버를 대여해주신 '(주)수학사랑'에 감사를 드린다.