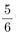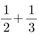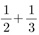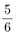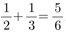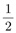수학사랑

이 글은 사단법인 전국수학교사모임의 회지인 '수학과교육' 2007년 7/8월호에 실렸던 필자의 글을 편집한 것입니다.

따짐이 : 선생님, 수학의 '수'는 우리가 흔히 말하는 그 '수' 지요?

선생님 : 그렇지. 설마 물이라는 뜻이겠니?

따짐이 : 헐 ~ '물' 끼얹은 듯 썰렁하네요. 어쨌든, 그럼 수학이 수에 대한 학문이라는 뜻인 것 맞네요?

선생님 : 말뜻은 그렇지. 하지만 수학이 수만 다루는 것은 아니라는 것은 너도 알지?

따짐이 : 원래는 그랬지요?

선생님 : 그것도 아니야. 수학이라는 표현은 우리나라, 일본, 중국 등에서 쓰이고, 영어의 mathematics

            처럼 유럽 언어에서는 수와는 직접 관련이 없는 말이 쓰이니까, 고대로부터 수학이라는 말은

            수와 도형의 연구를 함께 가리켰다고 할 수 있지. 학교에서 배우는 교과서 내용도 크게 수와

            도형에 대한 것으로 나눌 수 있지 않니?

따짐이 : 제가 하려는 말이 그 말이거든요. 수와 도형으로 잘 나가다가...

선생님 : 나가다가?

따짐이 : 문자. 그리고 ‘식’ 이라는 것이 나오는데 그것들의 정체를 잘 모르겠어요.

선생님 : 왜 그렇지?

따짐이 : 수끼리 계산하면 하나의 수가 답으로 나오잖아요? 그런데 식끼리 덧셈, 뺄셈, 곱셈 같은 계산

            을하면 답이 식이더군요.         

선생님 : 그게 어때서?

따짐이 : 예를 들면, 2x+3y에서 x-6을 빼면 답이 x+3y+6이 되잖아요?

선생님 : 그렇지.

따짐이 : 그리고 (2x+3y)-(x-6)도 식이고 x+3y+6도 식이죠?

선생님 : 그래.

따짐이 : 어차피 앞의 것도 식이고 뒤의 것도 식인데, 앞의 것을 뒤의 것으로 고치고서는 그걸 ‘계산’ 했다고 

            할 수 있나요?

선생님 : 식의 계산은 원래 그런 거니까.

따짐이 : 2+5를 계산해서 7이라고 할 때는, 그 사이에 분명히 다른 점이 있지요. 2+5는 하나의 수가 아닌데

            7은 하나의 수이니까.

선생님 : 글쎄... 그럼 이건 어때?

따짐이 : 뭐요? 

선생님 : 

따짐이 : 그래서요?

선생님 : 답이라고 하는 말인데, 그게 하나의 수인가? 5를 6으로 나누라는 뜻 아닌가?

따짐이 : 응? 그러고 보니 그런 것 같기도...

선생님 : 사실은 그렇지 않아.

따짐이 : 그, 그렇죠. 는 하나의 유리수인데, 그것을 그렇게 표현하는 것뿐이니까. 수직선에 찍어보면

            는 하나의 점에 불과하잖아요?

선생님 : 그럼 은? 그건 수직선에 찍으면 한 점이 아닌가?

따짐이 : 음...아무래도 제가 단순했나 보네요. 

선생님 : 그래. 에서, 좌변이건 우변이건 사실은 하나의 수를 말하는데 표현 방법이 다른 뿐이지. 

따짐이 : 그럼 의 ‘표현 방법을 고쳐서’ 로 만드는 것을 가리켜 덧셈을 한다고 하는 이유는

            무엇인가요?

선생님 : 덧셈이 원래 그런 거니까. a+b의 형태를 갖는 것을 c의 형태를 갖도록 고치는 것을 가리켜, a와 b를

            더하여 c를 계산했다고 하는거지.

따짐이 : 뭔가 내용이 없는 듯한 느낌이.... 

선생님 : 하지만   과 같은 등식은 분명히 내용을 담고 있어.