|
왜 함수를 그렇게 정의하는가?
작성자 : 수학사랑|조회수 : 11435 |
따짐이: 선생님, 함수는 무엇인가요? 선생님: 고등학교 1학년 교과서에 있는 대로, 집합 X에서 집합 Y로 가는 함수란, X의 원소에 Y의 원소를 꼭 하나씩 짝지어 주는 대응이지. 따짐이: 아래 그림처럼, X에서 남는 것도 없고 X에서 동시에 두 개와 대응하는 것도 없는 대응을 말한다는 거죠? Y에서는 상관 없고요.
선생님: 잘 아는군. 하지만 진짜 질문은 그게 아니겠지? 따짐이: 우선, 왜 X, 그러니까 함수라면 정의역이 될 집합에 대해서만 제약이 있고 Y, 즉 공역이 될 집합에는 제약이 없는 거죠? 선생님: 그 함수라는 게 결국 일차식이나 이차식, 분수식 같은 것을 가리킬 수 있게 뜻을 정한 것이니까. 따짐이: 함수가 원래 ‘식’ 이라는 건가요? 그런데 어떻게 해서 ‘대응’ 운운하게 된 것일까요? 선생님: 예를 들어, 따짐이: 네. 선생님: 그런데, x 에다 어떤 수를 넣으면 답이 안 나오기도 하니? 따짐이: 아니오. 어떤 수를 넣든지 답이 나오긴 나오겠죠. 선생님: x 에다 어떤 수를 넣으면 답이 두 개 나오기도 하니? 따짐이: 하나의 수를 넣었는데 답이 두 개? 아니오. 선생님: 왜 아닐까? 따짐이: 선생님: 그래. 식이란 어떤 수(한 개 또는 여러 개)를 ‘입력’하면 단 하나의 ‘출력’을 내보내는 기계와 같은 것이지. 입력을 했는데 출력이 안 나오거나, 두 개 이상 나오거나 하면 별로 쓸모가 없을 거야. 따짐이: 잠깐!
따짐이: 그러니까, 함수의 뜻에서 대응의 ‘화살표’가 출발하는 X쪽에 남는 것도 없고 화살표가 두 개 이상 나가는 것도 없어야 한다는 조건은, 항상 답이 한 개씩 나오는 일차식이나 이차식, 분수식 같은 것을 염두에 둔 것이라는 거죠? 선생님: 그래. 따짐이: 그럼, 그냥 식이라고 하면 되지 않을까요? 선생님: 그 ‘식’이라는 것이 애매하거든. 예를 들어 x 가 음수일 때는 -x 이고, x 가 0 이상일 때는 x 인 것으로 부분으로 나누어 정의하면 그것이 식일까? 잘 모르겠지. 하지만 기호로 |x| 라고 써 놓으면 완전히 식처럼 보인단 말이지. ‘x 이하인 정수 중에서 가장 큰 것’ 이라고 하면 식이라 할 수 없을 것 같았던 것도 [x] 처럼 써 놓으면 또 식이 되어 버린단 말이야. 따짐이: 그렇군요. 기호는 정하기 나름이니까. 선생님: 그래서 그런 식들을 ‘일반화’ 해서, 꼭 가지고 있어야 할 성질들만 가지고 함수라는 개념(용어)을 만들게 된 거야. 함수라는 개념에 될 수 있으면 많은 것들이 들어갈 수 있도록 말이야. 그래 놓고 함수에 대해 무엇인가를 증명하면, 일차함수, 이차함수, 분수함수, 삼각함수, |x|, [x] 할 것 없이 모든 함수에 대해 증명한 것이 되지. 따짐이: 그런데 함수가 결국 수를 입력해서 수를 출력하는 기능을 말하려 한 것이라면, 뜻을 말할 때 수에 수를 대응시킨다고 할 수는 없었을까요? 다시 말해 X 와 Y 는 무조건 실수의 집합이라고 하면 이해가 훨씬 쉬울 텐데... 선생님: 그렇게 하면 일단 따짐이: 역시 알고 보면 다 그럴 만한 이유가 있네요. 하지~만! 덕분에 함수의 뜻이 학생들에게 이해가 잘 안 된다는 거. 선생님: 그 대신 함수라는 개념은 많은 것들을 한꺼번에 이해할 수 있게 하는 매우 강력한 도구가 되었지. 게임을 하려고 해도 규칙을 알고 적용할 수 있을 때까지 어느 정도의 노력이 필요하듯이, 함수와 같은 기본 개념들의 뜻을 알고 이차함수나 무리함수 같은 것들을 그것에 비추어 생각할 수 있을 때까지 노력이 필요하지 않겠니? 그것은 수학적 개념들을 통합적으로 이해하고, 그래서 게임처럼 즐길 수 있게 되기 위한 관문이라고 할 수 있어. 이런 관문을 하나 통과할 때마다 세상을 더 넓게, 더 깊게 이해할 수 있게 하는, 예를 들어 함수라는 훌륭한 ‘아이템’을 얻을 수 있다는 것을 알아야 해. |
INTRODUCE PRODUCT
수학을 쉽고 의미있게 담아내는 수학교구 및 소프트웨어를 개발하여
수학문화의 대중화를 실천합니다.

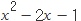 이 있다고 하자. 이 식은 x 에 0을 넣으면 -1, 1을 넣으면 -2, 3을 넣으면 2가 나오지?
이 있다고 하자. 이 식은 x 에 0을 넣으면 -1, 1을 넣으면 -2, 3을 넣으면 2가 나오지?
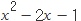
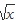 같은 식은 음수를 넣으면 답이 안 나오잖아요?
같은 식은 음수를 넣으면 답이 안 나오잖아요? 하지만 답이 안 나오는 입력값은 아예 제외하고 생각하는 것이 보통이야. 0으로 나누는 것은 제외하고 생각하듯이.
하지만 답이 안 나오는 입력값은 아예 제외하고 생각하는 것이 보통이야. 0으로 나누는 것은 제외하고 생각하듯이.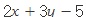 같은 두 개의 입력을 받는 식은 함수가 아니게 되지. 이런 경우 X는 두 수의 ‘순서쌍의 집합’이어야 하니까. 또, 도형에 그 도형의 넓이를 대응시키는 것(즉 X가 도형들의 집합)이라든가, 명제에 그것이 참인지 거짓인지를 대응시키는 것(즉 X는 명제의 집합, Y 는 {참, 거짓}) 같은 것도 함수로 보고 통합적으로 이해할 수 있는데 X 와 Y 를 수의 집합으로 제한하면 그럴 수가 없겠지.
같은 두 개의 입력을 받는 식은 함수가 아니게 되지. 이런 경우 X는 두 수의 ‘순서쌍의 집합’이어야 하니까. 또, 도형에 그 도형의 넓이를 대응시키는 것(즉 X가 도형들의 집합)이라든가, 명제에 그것이 참인지 거짓인지를 대응시키는 것(즉 X는 명제의 집합, Y 는 {참, 거짓}) 같은 것도 함수로 보고 통합적으로 이해할 수 있는데 X 와 Y 를 수의 집합으로 제한하면 그럴 수가 없겠지.






