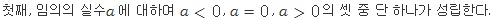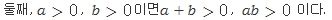|
왜 1은 2보다 작은가
작성자 : 수학사랑|조회수 : 11243 |
 이 글은 저널 '수학사랑' 57호(2006년 7/8월호)에 실렸던 필자의 글을 조금 고친 것입니다.
따짐이: 선생님, 고등학교 1학년(수학10-가) 교과서에 실수의 대소관계에 대해서 나와 있는데요. 선생님: 그렇지.
따짐이: 대체 무슨 이유로 그렇게 써 놓았는지 이해가 잘 안되거든요.
선생님: 뭐라고 써 있더라?
선생님: 그런데?
따짐이: 저는 이 문장들로, 예를 들어라는 표현의 뜻을 정의하고 있다고 생각하는데요. 다시 말해서 위 문장들을 가지고 부등호(>, <)의 뜻을 정의하고 있다고 이해했는데, 맞나요?
선생님: 맞아.
따짐이: 그런데 부등호의 뜻을 정의하는 말 속에 다시 부등호가 등장할 수도 있는 건가요?
선생님: 아니지.
따짐이: 아니지라뇨? 그럼 교과서가 잘못됐다는 것을 인정하시는 건가요?
선생님: 꼭... 그렇지만은 않아.
따짐이: 물론 그렇겠죠. 하지만 어떻게 된 일인지 알려 주시면 좋겠는데요.
선생님: 실수의 대소를 어떻게 정할 수 있을까? 예를 들어 1은 2보다 작은데 어떤 근거로 그렇게 말할 수 있을까?
따짐이: 수직선에 1이 더 왼쪽에 찍히... 는 것을 근거로 할 수는 물론 없겠고... 그냥 원래부터 정해져 있는 것 아닌가요?
선생님: 그 무수히 많은 것들이 서로서로 어느 것이 큰지 일일이 정해 놓을 수는 없지. 단, 자연수의 경우는 일일이 정했다고 할 수 있어. 1의 다음 수가 2, 2의 다음 수 가 3 등등으로 수 자체가 차례로 정의되기 때문에 그 순서로 점점 커진다고 하면 되니까.
따짐이: 오호, 그렇다면 자연수를 발판으로 해서 정해 나가면 되겠네요. 정수의 대소는, 음... 양의 정수끼리는 자연수의 대소를 그대로 따르고, 음의 정수끼리는 부호를 바꾼 다음 비교한 것의 대소와 반대인 것으로 정하고, 부호가 다른 것을 비교하면 항상 음의정수, 0, 양의 정수 순서인 것으로 하면...
선생님: 그렇지! 바로 그렇게 하지.
따짐이: 그리고, 유리수의 경우는... 에... 그렇지. 유리수는 분수로 나타낼 수 있으니까 두 유리수를 비교하려면 통분한 뒤에 분자를 비교하면 되겠군요. 분자는 정수이니까.
선생님: 옳지. 아주 좋아.
따짐이: 그러면 실수는? 그런데 실수가 뭐지?
따짐이: 하지만 정의되지도 않은 부등호가 이미 사용되고 있는데요?
선생님: 그래. 교과서란 항상 그런 어려움이 있지. 그것으로 공부하는 학생들의 수준에 맞추어야 한다는...
선생님: 그래. 그렇게 생각해 주면 교과서가 틀렸다고 말할 것까지는 없겠지. 그럼, 실수로서의 1이 2보다 작다고 말하는 근거는 무엇인지 이제 알겠니?
따짐이: 1-2 가 ‘음수’ 이니까!
선생님: 그래. 그렇게 생각하면 두 실수의 대소를 비교하는 문제를 풀 때 좌변의 수에서 우변의 수를 빼어 부호를 조사하는 것도, 단순히 그게 쉽기 때문이라기보다는 부등호의 정의에 따라 하는 일이라고 볼 수 있지. |
INTRODUCE PRODUCT
수학을 쉽고 의미있게 담아내는 수학교구 및 소프트웨어를 개발하여
수학문화의 대중화를 실천합니다.