수학사랑

다음은 94년도 대입수능 2차 시험에 출제된 문제이다. 

높이 1m인 담장이 반지름의 길이가 5m인 원 모양의 땅을 둘러싸고 있다.

광원이 원의 중심 O에서 2m 되는 지점에 수직으로 6m 되는 위치에 있을 때 이 광원에 의하여 생긴 담장의 그림자의 넓이는?

이 문제는 당시 많은 학생들이 어렵다고 느꼈던 문제이다.

왜냐하면 담장의 그림자가 직관적으로 타원이라고 생각했기 때문이다.

광원의 위치가 원의 중심에서 2m 떨어진 곳이라 타원이라고 생각하는 것은 아마 당연할지도 모른다. 이 문제 속에 숨어 있는 닮음의 지도에 대한 교훈을 생각해보자.
먼저 다음 왼쪽 그림과 같은 세 평행선 사이의 선분의 길이에 대한 문제는 모든 중학교 2학년 교과서에서 다룬다.

그러나 비례식에 의한 계산을 강조하느라 그 속에 숨은 수학적 진실을 외면한 것은 아닐까?

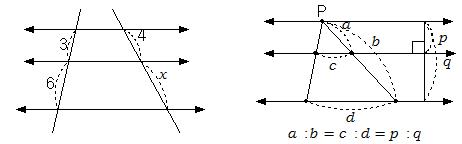
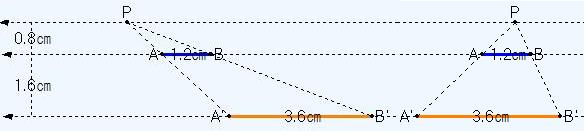
위 오른쪽 그림에서 점 P의 위치에 관계없이 c가 d로 확대되는 비율은 모두 평행선 사이의 거리의 비로 일정하다.

실제로 다음 그림에서 점 P의 위치에 따른 길이를 관찰해보자.

점 P의 위치에 관계없이 항상 황색 선분은 파란 선분의 3배이다. 

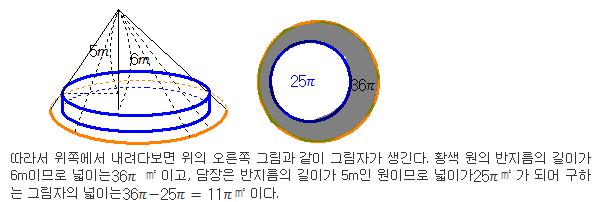
왜냐하면 평행선 사이의 거리의 비가 0.8 : 0.8+1.6=0.8 : 2.4 =1:3이기 때문이다.

직관적으로 점 P를 한쪽 방향으로 많이 옮기면 황색선이 길어질 것같지만 위의 실험에서 실제로 그렇지 않다는 것에 학생들이 놀랄 수 있으면 좋겠다. 

어떤 현상을 놀라움으로 받아들이면 자연스럽게 "왜 그럴까" 하는 의문이 생긴다.

바로 이 때 논리적인 설명이 필요하다.  

이것을 3차원으로 확장해 보자. 

아래 왼쪽 그림에서 광원이 지면과 평행한 평면 위의 어디에 있든지 담장 위 부분의 파란 원의 그림자는 위치는 변하지만 그 크기는 평행한 평면 사이의 거리로 결정되어 항상 일정하다.

즉 광원이 있는 평면과 담장 위 부분의 원을 품는 평면, 그리고 지면과의 거리의 비가 5:6 이므로 담장 위부분의 파란원은 5:6으로 확대된 황색 원 모양의 그림자를 만든다.

이 때 담장의 반지름의 길이가 5m이므로 황색 그림자의 반지름의 길이는 6m이다.

닮음변환의 내용을 아는 학생들에게는 쉬운 문제이기도 하다.

출제한 사람은 아마 많은 학생들이 맞칠 수 있는 문제라고 생각했을지도 모른다.

매너리즘에 빠져 문제 풀이에 치우치다가 본질을 놓치는 우를 범하지 않아야 한다는 교훈을 다시 한번 마음에 새겨본다.
그 후 이 내용을 직관적으로 관찰하고 실험할 수 있는 교구를 만들었고 1999년 중앙일보와 수학사랑 공동주최로 디자인포장센터에서 개최한 수학체험전에서 일본교구와 함께 전시했다. 
        
이 교구의 위쪽에 전구를 달고 이것을 어느 방향으로나 움직일 수 있도록하였고 중간 부분에 원 모양의 구멍을 뚫었다.

전구에서 나온 빛은 원 모양의 구멍을 통과하여 아래 검은 판에 하얀 원으로 나타난다.

이것을 잘 관찰하기 위해 아래 주변에 온통 검은 색을 칠해두었다.
사실 모든 교구가 다 놀랍지만 전구를 자유롭게 움직일 때 아래에 생기는 흰 원이 크기가 변하지 않고 위치만 다른 것을 관찰하게 되면 누구나 깜짝 놀랄 것이다.

이 교구는 지금도 체험전을 할 때마다 전시되는 데 이를 본 관람객이 놀랍게 받아들일 때 이 교구를 만들 때의 많은 어렵고 힘들었던 과정들이 보람으로 돌아온다.
한편 수학이란 무엇인가 흔들거나 움직일 때 변하지 않는 어떤 성질을 탐구하는 과정이라는 것에 놀라움과 경이로움울 느낀다.