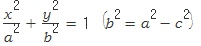수학사랑

평면 위에서 두 정점F, F‘으로 부터의 거리의 합이 일정한 점들의 집합이 타원이다. 두 정점F(c, 0), F‘(-c, 0)으로부터의 거리의 합이 2a(a〉c〉0)인 타원의 방정식은

이다. 타원은 ellipse를 번역한 것이며, 한자로는 橢圓이라고 쓴다.

ellipse → 橢圓 → 타원

ellipse는 Perga의 Apollonius(약 262 B.C.～약 190 B.C.)가 만든 용어로 알려져 있다. ellipse는 그리스어 en과 leipein으로부터 온 것으로, '부족하다'를 의미한다고 한다. 다음 그림에서 각α와 각β를 비교하면, α〉β임을 알 수 있다. 즉, β는 α에 비해서 부족하다고 볼 수 있다. Apollonius는 대체로 이런 이유에서 ellipse라는 용어를 만든 것으로 보인다(Schwartzman, 1994).

ellipse를 번역하면서 '橢圓'이라는 용어를 만든 것이다. 이 용어는 羅雅谷(Jacques Rho, 1593-1638)이 편집한 책《測量全義(측량전의)》(1631년)에 ellipse의 번역어로 나타난다고 한다. 橢圓대신 楕圓(타원)으로 쓰기도 한다. 楕는 橢의 약자이다. 橢또는 楕에는 '둥글 길쭉하다'는 뜻이 있다. 따라서 橢圓에는 '둥글 길쭉한 원'이라는 뜻이 있다. 생긴 모습이 둥글 길쭉했기 때문에 '橢圓'이라고 했을 것으로 보인다. 그러나 橢의 자의(字意)를 해석하여, 橢가 나무를 잘라내고 남은 그루터기를 의미하는 것으로 보기도 한다. 이러한 해석은 아마도 나무의 윗부분을 밑면과 평행하지 않게 잘랐을 때, 남아있는 그루터기의 단면에서 橢를 만든 것이라고 보는 것이다(片野善一郞, 1991).