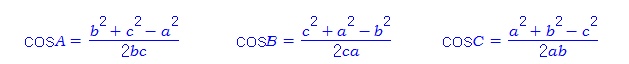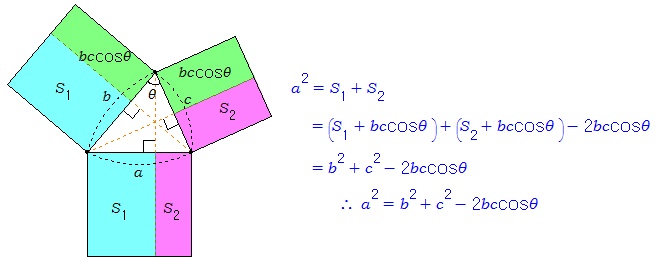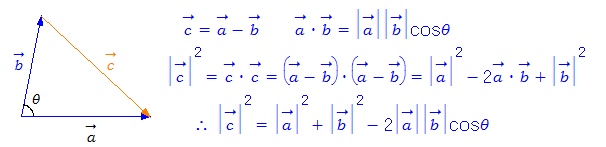|
코사인법칙/Law of Cosines
작성자 : 수학사랑|조회수 : 25435 |
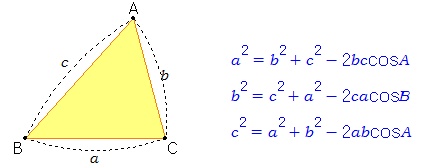
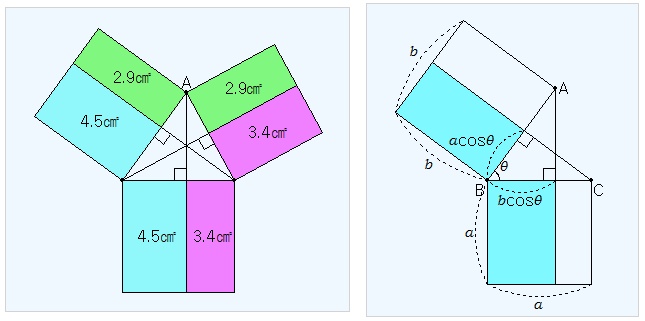
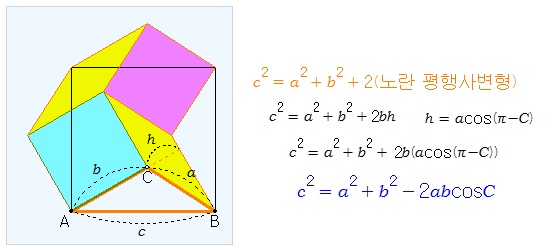
임의의 삼각형 ABC에서 다음이 성립한다. 이것은 피타고라스 정리의 일반화로서 코사인법칙이라고 한다. 위의 공식은 두 변과 끼인각으로 대변의 길이를 구할 수 있는 식이다. 이 식을 다음과 같이 변형하면, 세 변의 길이로부터 세 각의 코사인 값을 구할 수 있는 식이 된다. (증명 1) 삼각비의 정의를 이용하여 증명해 보자. 다음 왼쪽 그림의 점 A를 움직여 보면서 어떤 부분의 넓이가 서로 같은지 알아보자. 직각삼각형이 되도록 해 보자. 또 오른쪽 그림의 점 A를 움직여 보고 그 이유를 생각해 보자.
위의 오른쪽 그림에서 색칠한 두 도형의 넓이는 둘다abcosθ이다. 또 색칠한 사각형의 넓이는 두 벡터 BA, BC의 내적이기도 하다. 위의 내용을 예각삼각형 ABC에 대하여 적용하면 다음과 같다. 아랫쪽 정사각형의 넓이는 위쪽 두 정사각형의 넓이의 합에서 2개의 녹색직사각형의 넓이를 빼면 된다. 앞의 그림의 점A를 움직여 둔각삼각형을 만들고 이 경우의 증명을 생각해 보자.
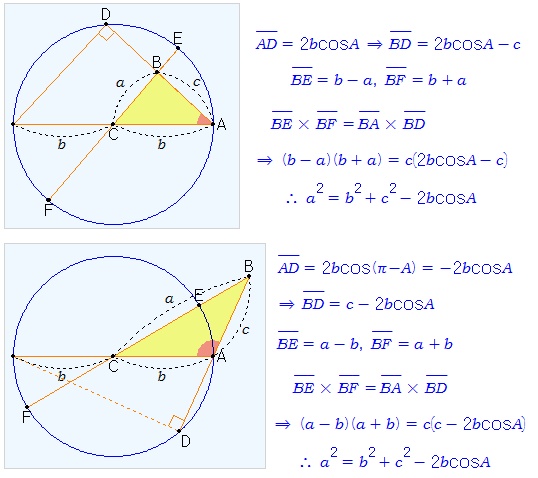
(증명 2) 원과 비례 (방멱정리, Power theorem)를 이용하여 증명해 보자. 삼각형 ABC의 꼭지점 C를 중심으로하고, 점 A를 지나는 원을 그린다. 삼각형의 변의 연장선과 원이 만나는 점들을 선분으로 잇는다. 점 B를 움직여 보자.
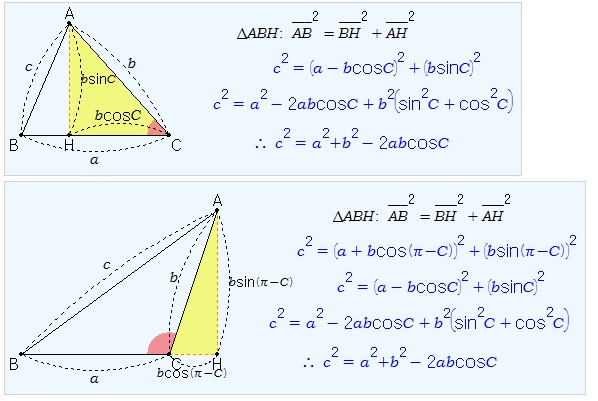
(증명 3) 피타고라스의 정리와 삼각비를 이용하여 증명해 보자. 점 A를 움직여 보자.
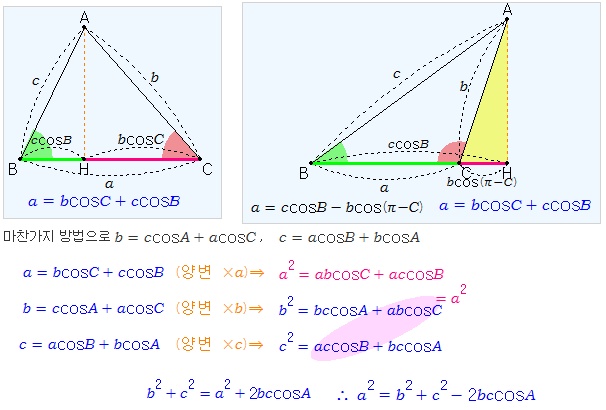
(증명 4) 정사영의 길이와 삼각비를 이용하여 증명해 보자. 점 A를 움직여 보자.
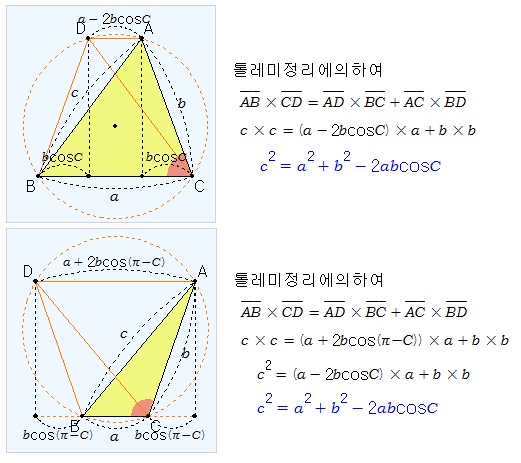
(증명 5) 톨레미 정리와 삼각비를 이용하여 증명해 보자. 점 A를 움직여 보자.
(증명 6) 점 C를 움직이면서 유클리드의 증명을 이해해 보자. 또 직각삼각형이 되게 해 보자.
점 C를 선분 AB 위에 놓아보자. 이 때, ∠C=π이고, 선분에서도 코사인법칙이 성립한다.
다음은 유클리드 증명으로 만든 테셀레이션이다. 점 C를 움직여보자.
(증명 7) 벡터의 내적을 이용하여 증명해 보자.
|
MATH STORIES
수학백과사전에서 칼럼까지
수학사랑에서 알려드리는 수학과 관련한 이야기들