이 글은 저널 '수학사랑' 50호(2005년 5/6월호)에 실렸던 필자의 글을 조금 고친 것입니다. 따짐이: 선생님, 질문 있어요.
선생님: 뭐지? 기대되는 걸?
따짐이: 그 이야기 있잖아요. 아킬레스와 거북이 이야기.
선생님: 그게 왜?
따짐이: 거기서 뭐가 잘못되었는지 모르겠어요.
선생님: 잘못된 것 같기는 하니?
따짐이: 그 이야기는, 아킬레스가 거북이가 있던 자리까지 가면 거북이도 조금이나마 앞으로
나아가고, 또 그 자리까지 가면 또 아주 조금이지만 거북이가 앞으로 나아가고, 그런 식으로 끝없이 계속된다는 거잖아요? 
선생님: 그렇지.
따짐이: 그런데 실제로 뛰어 보면 왜 끝이 나는 거죠?
선생님: 그래서 무한이라든지, 끝이 없다는 말을 할 때는 조심해야 해. 사실 수학에서 어려운 부분은 대개 무한에 관련되어 있지.
따짐이: 그 말씀은, 제가 끝없이 계속된다고 한 말에 뭔가 문제가 있다는 건가요?
선생님: 끝없이 계속된다는 것은 무엇이 계속된다는 거지?
따짐이: 따라가고, 또 따라가는 과정이 계속된다는...
선생님: 그래, 그것은 실제로 끝없이, 즉 무한히 계속된다고 말할 수 있지.
따짐이: 예? 끝이 나잖아요?
선생님: 아니야. 네가 방금 끝난다고 했는데, 그 때 끝난다는 말은 무슨 뜻이지?
따짐이: 그건, 그러니까... 맞아요. 어느 일정한 시간까지만 계속되고 그 이후에는 일어나지 않는다는 뜻이죠. 다시 말해 걸리는 시간이 유한이라는...
선생님: 그 두 가지가 동시에 성립할 수는 없을까? 즉, 하나는 거북이가 있던 곳까지 따라가고 그 동안 조금 앞으로 간 거북이를 또 따라가는 일이 무한히 계속된다는 것, 또 하나는...
따짐이: 그 일이 유한한 시간 안에 끝난다는 것?
선생님: 그렇지.
따짐이: 하나는 무한히 계속된다는 것, 또 하나는 유한한 시간 안에 끝난다는 것인데 그것이 동시에 일어난다?
선생님: 그렇게 말하면 혼동하게 되는 거야. 무한한 것은 무엇이고, 유한한 것은 무엇이냐를 구별해야지.
따짐이: 그러니까, 따라가고 또 따라가는 일의 '회수' 는 무한이지만 그 때 걸리는 '시간'은 유한이라고 말씀하시려는 건가요?
선생님: 바로 그거야. 그것이 그 역설을 극복하는 열쇠가 되지.
따짐이: 무한히 많은 일을 하는데 유한한 시간이 걸릴 수 있을까요?
선생님: 무한히 많은 것을 더한다고 해서 그 합이 꼭 무한이라는 법은 없지.
따짐이: 아, 그렇다. 무한급수의 합이라도 유한이 될 수 있지.
선생님: 이 경우에는 유한인지 아닌지 확인해 볼까?
따짐이: 좋아요. 우선 아킬레스의 속력이 초속 10미터, 거북이의 속력이 초속 1미터라고 하고, 아킬레스를 100미터 뒤에서 출발시켜 보죠.
선생님: 거북이치고는 꽤 빠른 걸?
따짐이: ...
선생님: 어쨌든, 그러면 아킬레스가 거북이가 있던 곳까지 가는데 10초가 걸리겠지.
따짐이: 그리고 그 10초 사이에 거북이는 10미터 앞으로 가고...
선생님: 그 10미터를 다시 따라잡는데 1초.
따짐이: 그 1초 사이에 거북이는 1미터 앞으로 가고...
선생님: 그 1미터를 다시 따라잡는데 0.1초.
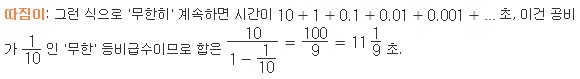 선생님: 정말 유한이군.
따짐이: 따라가는 과정은 무한히 계속된다고 볼 수 있지만, 그 때 걸리는 시간은 유한이다. 다시 말해 무한히 많은 것들을 합해서 유한한 값이 나온다는 것이 핵심이군요.
선생님: 그래. 바로 그렇지. 그런데 학교에서 그 내용 배우지 않니?
따짐이: 배웠죠. 그러니까 공식으로 합도 구했죠.
선생님: 그런데 그것을 배울 때 무한히 많은 것을 합해서 유한한 값이 나온다는 것이 이상하다는 생각을 해 본적은 없니? 아킬레스와 거북이 이야기(일명 제논의 역설)가 이상하다면, 그것도 이상하다고 생각해야 하는데 말이야.
따짐이: 글쎄요. 그냥 그렇게 된다고 이해하고, 바로 합 구하는 연습으로 넘어가서...
선생님: 그래서 그렇게 상식과 어긋나는 사실을 공부하는데도 별다른 느낌 없이 지나갔다는 말인가?
따짐이: ...
선생님: 만약 그랬다면, 선생님도 문제지만 학생들에게도 문제가 있기는 마찬가지야. 어떤 지식을 배울 때는 자기가 이미 가지고 있는 상식이나 지식에 비추어 생각해 볼 필요가 있는데, 수학 책에 있는 것을 무비판적으로 받아들인 것이지. 기존의 상식이나 지식이 새로운 지식과 갈등을 일으킬 때, 그래서 의문이 생길 때, 그 때가 바로 새로운 것을 제대로 배울 수 있는 가장 좋은 기회인데 말이야 |