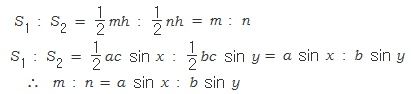|
각의 이등분선의 일반화
작성자 : 수학사랑|조회수 : 14365 |
이미 잘 알려진 각의 이등분선의 성질과 증명은 다음과 같다. 이 증명을 오랫동안 기억하고 있었지만 다른 증명 방법을 찾을 생각은 하지 못하였다. 얼마전 연수 강의 준비를 하다가 문득 이 정리를 일반화해 보는 생각을 하였다. 이를 증명하는 과정에서 위의 평행선을 이용한 증명은 매우 한정적인 방법이고 삼각형의 넓이를 이용하는 방법이 일반적임을 알게 되었다. 물론 x=y 이면 m : n=a : b 가 되어 각의 이등분선의 성질이 된다.
한편, 외각의 이등분선의 성질과 증명은 다음과 같다.
외각의 이등분선도 마찬가지 방법으로 일반화할 수 있고 삼각형 ABQ와 ACQ의 넓이를 이용하여 증명할 수 있다. |
INTRODUCE PRODUCT
수학을 쉽고 의미있게 담아내는 수학교구 및 소프트웨어를 개발하여
수학문화의 대중화를 실천합니다.