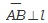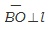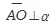수학사랑

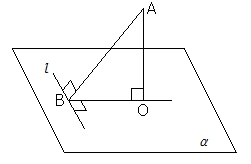
평면 α밖의 한 점 A, 평면 α위의 한 직선 l 에 대하여, 점에서 평면에 내린 수선의 발을 O, 점에서 직선 l 에 내린 수선의 발을 B라고 하면

이다. 또 점 A에서 직선 ㅣ에 내린 수선의 발은 점 B와 일치하므로

이다. 한편, 평면α위에서 점 B를 지나 직선 ㅣ에 수직인 직선을 긋고 점 A에서 이 직선에 내린 수선의 발은 점 O와 일치하므로

이다. 이 내용이 삼수선의 정리이다.

삼수선의 정리는 theorem of three perpendiculars를 번역한 것이다. 삼수선과 정리를 한자로는 각각 三垂線, 定理라고 쓴다.

theorem of three perpendiculars → 三垂線의 定理 → 삼수선의 정리

perpendicular는 본래 '수직의, 직교의'라는 뜻을 가진다. 이것으로부터 '垂線(수선)'이라는 뜻이 생겨난 것이다. perpendicular는 목수들이 수직을 알아보기 사용했던 다림줄(plumb line)을 의미하는 라틴어 perpendiculum에서 온 것으로 알려져 있다(Schwartzman, 1994). 이것을 번역하면서 '垂線'이라는 용어를 만든 것이다. 垂에는 '드리우다, 아래로 늘이다'라는 뜻이 있다. 그래서 수선에는 '아래로 늘여진 선'이라는 뜻이 있다. 그러나 수선이 항상 아래로 늘여진 것만은 아니다.

일반적으로는, 수학에서 두 직선이 서로 수직일 때 한 직선이 다른 한 직선의 수선이다. 垂線은 '垂直인 直線'을 간단히 한 것이다. theorem은 '定理'이고, three perpendiculars는 '세 垂線'이므로, theorem of three perpendiculars는 '세 수선의 정리'이다. 여기서 '세 수선'을 한자 三을 사용하여 '三垂線'으로 바꾼 것이 '三垂線의 定理'이다. '세 개의 수선에 대해 성립하는 정리'라는 의미에서 '삼수선의 정리'라고 하는 것이다.