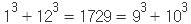간단한 숫자퍼즐과 페르마의 정리의 비슷한 오일러의 가설 얼마 전 <수학세상 가볍게 읽기, 데이비드 애치슨, 황선욱 역, 한승, 2007>이란 책을 읽었다. 거기에서 페르마의 정리와 비슷한 오일러의 가설 이야기가 나온다. 그 내용은 다음과 같다.
| 
|
『1753년에 오일러는 다음 등식을 만족시키는 자연수 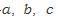 가 존재하지 않는다는 사실을 증명하였다. 가 존재하지 않는다는 사실을 증명하였다.
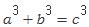
달리 말해서 자연수의 범위에서만 생각하면 세제곱수 2개를 더한 값이 다시 세제곱수가 되는 경우는 없다. 이것은 페르마의 마지막정리의 특수한 경우로 지금까지는 별 이상이 없다.
그런데, 몇 년이 지난 후에 오일러는 다음과 같은 가설을 내놓았다.
네제곱수 3개를 더한 값이 다시 네제곱수가 되지 않으며,
5제곱수 4개를 더한 값이 다시 5제곱수가 되지 않으며,
6제곱수 5개를 더한 값이 다시 6제곱수가 되지 않는다. …… 이와 같은 주장을 확인하기 위해 사용되는 수들이 아주 빠른 속도로 커지기 때문에, 여러 해 동안 오일러의 가설을 아무도 증명하지 못했을 뿐만 아니라, 이 가설을 뒤엎는 반례를 찾은 사람도 없었다.
그러다가 오일러가 이 가설을 세운지 200여년이 지난 1966년에 와서야, 마침내 랜더(L.J, Lander)와 파킨(T.R. parkin)이 아래와 같은 5제곱수 4개를 더한 값이 다시 5제곱수가 되는 반례를 찾았다. 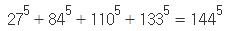
이와 같이 수학에서도, 틀린 가설이 아주 오랫동안 틀린 채로 남아있을 수 있다.
1986년 미국 하버드 대학의 노암 앨키스(Noam Elkies)가 다음과 같은 네 제곱수의 반례를 처음으로 밝혔다. 
이 글을 읽으면서 떠오르는 숫자퍼즐이 있어 소개하고자 한다. 문제1.
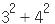 과 같이 표현한 것을 연속된 두 자연수의 제곱의 합이라고 하자. 과 같이 표현한 것을 연속된 두 자연수의 제곱의 합이라고 하자.
(1) 연속된 두 자연수의 제곱의 합이면서 연속된 세 자연수의 제곱의 합이 되는 수 중 가장 작은 자연수를 구하여라.
(2) 연속된 두 자연수의 제곱의 합이면서 연속된 세 자연수의 제곱의 합이 되는 수를 구하여라. 문제2.
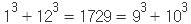 는 두 수의 세제곱으로 나타내는 방법이 2가지인 수 중 가장 작은 수이다. 는 두 수의 세제곱으로 나타내는 방법이 2가지인 수 중 가장 작은 수이다.
(1) 두 수의 제곱으로 나타내는 방법이 2가지인 수를 구하여라.
(2) 이와 같이 두 수의 세제곱으로 나타내는 방법이 2가지인 다른 예를 찾아보아라. |

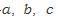 가 존재하지 않는다는 사실을 증명하였다.
가 존재하지 않는다는 사실을 증명하였다.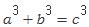
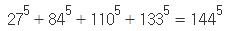

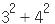 과 같이 표현한 것을 연속된 두 자연수의 제곱의 합이라고 하자.
과 같이 표현한 것을 연속된 두 자연수의 제곱의 합이라고 하자.