수학사랑

80년대초 지금 대학로에 있는 한 여자중학교에 근무할 때이다.
          
수학교사가 되어 처음 0.99999...=1 임을 증명하고,

수업을 마쳤는데 그날따라 다른 날과 달리 기분이 산뜻하지 못하였다.

무언가 아이들의 마음을 완전히 충족시키지 못했기 때문이다. 
쉬는 시간 창문 너머로 한 여학생이 교무실로 오고 있었다.

왠지 좀 불길한 예감이 들었다
그 학생은 당시 전교 1등인 긴머리의 너무도 예쁘고 착하고 거의 질문이 없는 학생이었다.
"반장이니까 담임선생님께 가는 걸꺼야" 라고 생각하고 있는데 점점 나에게로 오는 것을 직감적으로 느낄 수 있었다.

"선생님, 0.99999…가 정말 1인가요? "

"1과 거의 같지만 그래도 아주 조금 작은 것 같아요!"
수업 시간의 논리적인 증명은 이해가 가지만

 0.99999…는 아무리 9가 계속되어도 1보다 작지 않느냐는 것이다.
"헉! 올 것이 왔구나"
사실 수업 시간에 설명한다고 했지만...

그 설명이 충분치 못하다는 것을 난 알고 있었다. 

솔직히 말하자면 더 잘 설명할 지식과 지혜와 경험이 없었다.

대체로 3년쯤 된 교사는 잘 모를수록  제 잘난줄 알고 학생들 앞에서 얼마나 절대적인 모습으로 행동하는가?
그러니 이 학생은 교실에서 보다 무엇인가 확실한 답변을 듣고 싶어 큰 기대를 가지고 왔을 것이다.

그러나 이제 더 이상 어설픈 설명이 필요 없음을 너무도 잘 알고 있었기에  내가 던진 한마디...
"나도 그렇게 생각해...윤정아!"

돌아가는 윤정이의 축 쳐진 뒷모습이 오랫동안 마음에 걸렸다.
그날은 왜 그리도 내 자신이 초라하게 보였는지...

친구와 함께 밤 늦도록 쓴 소주를 마시면서 수학교육에 대하여 고민했었다.

사실 증명과정에서도 소숫점 아래 무한히 계속되는 9들이 없어진다고 했는데 이것도 여간 개운치 않은 곳이다.

유한개라면 당연하지만 무한개인데...

자연수집합과 홀수집합이 일대일대응이 되는 무한인데... 과연 가능할까?

물론 이 문제를 고등학교 수열의 극한으로 보내면 큰 문제가 없다.

그러나 이것은 우리 힘으로는 어려운 일이다. 

궁색하지만 교사적인 해결책을 찾아야만 했다.

이 문제의 핵심은 학생들의 직관과 논리의 충돌이다.

논리적으로 수긍할 수 밖에 없은데 직관이 허락하지 않는 것이다.

사실 수학을 공부하면서 이런 일은 흔한 것이다.

특히 나의 경우 대학에서는 더욱 그러했다.

직관적인 느낌 없이 오로지 논리로만 존재하는 그 많은 정의와 정리들... 재미있을 리가 없다.

난 이 문제를 학생들이 직관의 동의 없이 무엇인가를 받아들이는 기회로 삼을 수 밖에 없다는 생각을 했다.

"애들아, 1광년이 얼마나 될까?"  " 빛이 1년 동안 가는 거리요"
"100m는 직관적으로 느낄 수 있지만 1광년은 도저히 직관적으로 느낄 수 없단다."
"세상에는 직관적으로 확실하게 느껴지지 않지만 받아들여야 하는 지식들이 많단다"

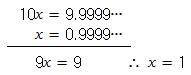
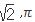사실  등도 모두 순환하지 않는 무한소수로서 그 실체를 아무도 직관적인 동의를 할 수 없지만 기호를 사용하여 논리적으로 인정하고 받아들이고 있는 것이다.
우주와 인간의 탄생...우리 현실 앞에 있지만 직관적으로 생각하면 할 수록 더욱 느껴지지 않는 인간의 한계..

이것을 넘어서 학문의 세계로 나아가야 한다.

아이들에게는 많은 위로와 격려가 필요할 것이다.