수학사랑

두 원의 방정식을 주고 공통현의 방정식을 구하는 문제는 학력고사 시절 거의 매년 출제되었던 중요한 내용이었다.

" 원의 방정식의  x, y의 제곱항의 계수가 모두 1일 때,

두 원의 방정식을 변변 빼면 x의 제곱, y의 제곱 항은 없어지고 x, y의 일차방정식이 남아 직선이 되는데 이것이 공통현의 방정식이다."

몇 년 후 과학고등학교 학생들과 두 도형의 교점을 지나는 도형의 방정식에 대한 공부를 하고 공통현의 방정식을 그 예로 들었다.
그 순간 한 학생이 손을 들고 "선생님! 두 원이 만나지 않을 때에도 두 원의 방정식을 빼면 일차식이 남아 직선의 방정식이 됩니다. 이 직선은 무엇인가요?"

난 둔기로 뒤통수를 맞은 듣 잠시 멍하게 있고 말았다. 

지금까지 이 내용을 그리도 많이 가르쳤지만 난 이 경우를 생각조차 하지 못했다.

물론 그 때의 학생들 누구도 그런 질문을 하지 않았다.

난 질문한 학생의 머리를 쓰다듬으며 학생들 앞에서 칭찬 공세를 퍼부었다.

"선생님은 지금까지 그 생각을 한 번도 못했는데...정말 훌륭하구나.." 
학생들이 그 아이에게 관심을 두는 사이...

좀 어색하고 볼멘 목소리로  "선생님이 공부하여 알려 줄께.."라고 말했던 슬픈 추억이 있다.

그 후 각고의 노력을 했지만 쉽게 찾아지지 않았다.

약 3개월 정도 지난 어느날  당시 구독하던 일본 잡지에서 우연히 ' 근축 (Radical Axis) ' 이라는 내용의 글 속에서 그 답을 찾아내었다.

 원이 만날 때에는 공통현이지만 원이 만나지 않을 때에도 직선을 볼 수 있다.

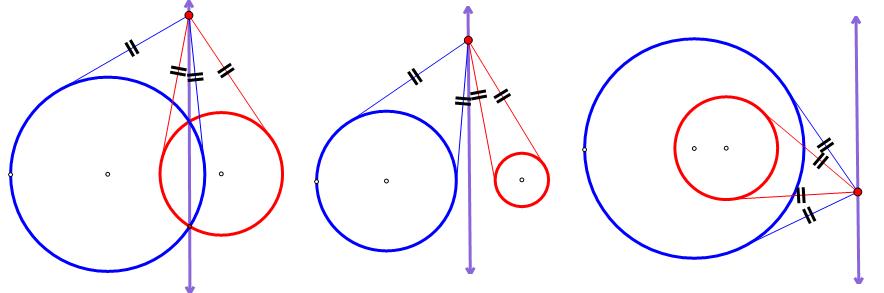
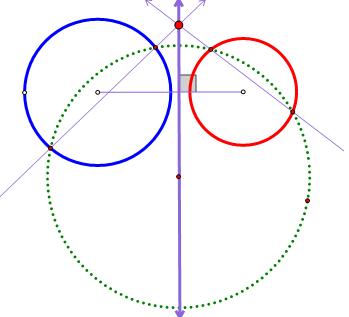
원이 만나든 만나지 않든 이 직선 위의 임의의 점에서 두 원에 그은 접선의 길이가 같다.

즉, 두 원의 원의 파워 가 같다.

다시말하면 두 원에 그은 접선의 길이가 같게 되는 점의 집합 또는 두 원의 파워가 같은 점의 집합이 바로 근축이다.

자 이제 근축의 방정식은 두 원의 방정식을 빼면 된다.

즉, 좌표평면에서는 쉽게 근축을 그릴 수 있다.

그렇다면 논증기하적으로는 어떻게 작도할 수 있을까?

이것이 궁금했다면 수학더듬이가 매우 좋은 편이다.  수학을 잘 할 수 있는 사람이다.

다음 그림을 보고 생각해 보기 바란다.

공통현은 근축이라는 새로운 이름이 하나 더 있는 셈이다.  

공통현에 대한 슬픈 추억은 근축을 만나는 계기가 되었다.

그 때 질문을 던진 한성과학고 제자는 지금쯤 무엇을 하고 있을까?