수학사랑

사실 이 내용을 제대로 이해하려면 아래 그림과 같이 한 점 P와 원이 있을 때 

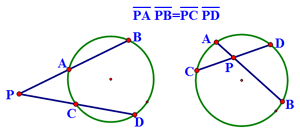
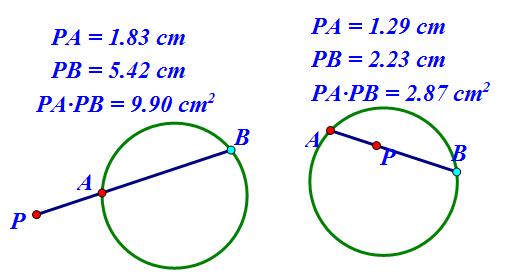
점B를 원 위에서 마음대로 끌어 선분 PA와 선분 PB의 값이 변해도 "두 선분의 곱 PA ×PB 의 값은 항상 일정하다."는 것을 알아야 한다.   

                 
 따라서 원과 비례는 위의 그림과 같이 "원 위의 점 B의 위치에 관계없이 항상 의 값이 일정하다"를 강조하여 가르쳐야 하지 않을까하는 생각을 해본다.

원과 비례는 "평면 위의 있는 한 점과 원의 기하적인 상황에 대하여 파워(Power)라는 실수가 하나 대응"하는 것을 의미한다.

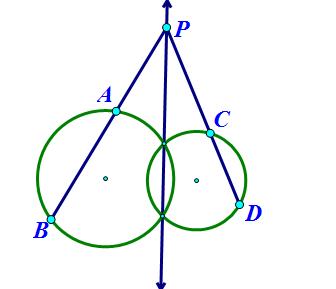
다음은 원과 비례를 공부한 후 모든 교과서에서 다루는 문제이다.

      
여기서  PA ×PB =PC×PD임을 증명하는 문제이다.

이것을 식으로 증명만하고 간다면 참 아쉬움이 많다.

즉, 이 그림에 숨은 기하적인 의미는 무엇일까? 
"두 원의 교점을 지나는 직선 위의 임의의 점 P에서 두 원에 그은 접선의 길이가 같다"는 뜻이다.

즉, "두 원에 대한 파워가 같다"라는 뜻이다.
다시말하면, 두 원에 그은 접선의 길이가 같은(파워가 같은) 점들의 모임이 교점을 지나는 직선이라는 뜻이다.
중학교 1학년 때 두 원의 위치관계를 배웠다는 것을 일깨워 주면서 이 내용과 결부하여 새로운 문제를 생각해 볼 수 있는 시간을 주면 어떨까?

아마도 아이들의 생각의 문을 활짝 열 수 있는 기회가 될 것이다.

"두 원이 위치관계에 따라 접선의 길이가 같게 되는 점들의 모임은 어떻게 될까요? 생각해 오세요!"라고 숙제를 내는 것도 좋을 듯하다.

또는 다음과 같은 질문을 해 보자.

" 두 원이 접할 때는 접선의 길이가 같게 되는 점들의 모임은 어떤 도형이 될까?"
" 두 원이 만나지 않을 때 접선의 길이가 같게 되는 점들은 어떤 도형(직선)이 될까?
" 또 그런 직선은 어떻게 작도할 수 있을까?"
더 나아가...
"원과 비례를 공간으로 확장하면 어떻게 될까?"
"공간에 한 점과 구가 있을 때 원과 비례를 증명해 보자."
.......
끝으로 파워(Power)라는 말은 방향에 따른 곱이라는 뜻의 방멱(方; 방향, 冪; 계속 곱하기)이라고 번역할 수 있으나 한자 말이라 좀 아쉽다. 멋진 우리 말 이름이 있었으면...