|
왜 부등식의 성질은 등식의 성질과 다른가
작성자 : 수학사랑|조회수 : 11050 |
||
따짐이: 지난번에 등식의 성질에 대해 말씀해 주신 것 감사했어요. 등식의 성질이라 부르 선생님: 그렇게 요약할 줄 아는 것을 보니 정말 잘 이해했나 보구나. 오늘은 무슨 질문이지? 따짐이: 등식의 성질이 그런 것이면, 부등식의 성질도 비슷한 것인가요? 선생님: 글쎄... 보기에 따라서는... 따짐이: 그것들이, 다 똑같은데 부등식은 양변에 ‘음수’ 를 곱하면 부등호의 방향이 바뀐다 선생님: 그래서? 따짐이: 그게 과연 뭔가 근본적으로 비슷한 것이라서 그런 건가요, 아니면 우연히 결과만 선생님: 너는 어떻게 생각하니? 따짐이: 등식의 성질과 부등식의 성질은 뭔가 근본적으로 다른 것이라고 생각되는데요. 선생님: 왜 그렇지? 따짐이: 등식의 성질은 하나의 깨끗한 법칙이죠. 같은 수에 같은 일을 하면 그 결과가 같다. 선생님: 다른 건 사실이지. 등식은 ‘같음’에 대한 이야기이고, 부등식은 ‘순서’에 대한 이야 따짐이: 넓게 생각한다면... 등식의 성질에서, 양변에 같은 수를 더하거나 빼거나 곱하거나 선생님: 그래. 따짐이: 음... 선생님: 그렇지!
선생님: 없지. 하지만 어떨 때는 그렇게 말할 수 있지.
선생님: 그렇지. 바로 그래. 따짐이: 그런데 그건 부등식의 성질을 함수 기호를 써서 나타낸 것밖에 안 되는 것 같은데요? 선생님: 아니지. 어떨 때는 대소관계가 그대로고, 어떨 때는 대소관계가 바뀌는데, 그 ‘어 따짐이: 글쎄, 저한테는 별로 분명하지가 않... 아, 그렇군! 결국 함수가 어떤 것이냐에 따 선생님: 바로 그거야. 어떤 함수는 대소관계를 그대로 유지시키고(어려운 표현으로는 ‘보 따짐이: 그렇다면... 어떤 수를 더하거나 빼는 함수, 양수를 곱하거나 나누는 함수는 모두 선생님: 그렇지. 따짐이: 이렇게 말하니까 뭔가 있어 보이네요. 선생님: 하지만, 그것뿐이라면 별로 쓸모는 없어. 어떤 수를 더하는 것이 대소관계를 보존 따짐이: 듣고 보니 또 그렇네.
따짐이: 호오, 그렇다면... 어떤 수를 더하거나, 빼거나, 곱하거나, 나누는 것은 모두 일차 선생님: 아주 말이 잘 되지. 수학 용어로는 우리의 ‘대소관계를 보존하는 함수’ 를 ‘순증가 따짐이: 어떤 수를 더하거나 빼는 함수는 순증가함수, 양수를 곱하거나 나누는 함수도 순 선생님: 그래. 이것도 결국 함수에 관한 문제야. 함수의 정의 자체는 ‘같음’ 을 보존한다는 따짐이: 원래 더 컸으면 순증가함수를 작용한 뒤에도 더 크다? 선생님: 그래. 꼭 대소관계뿐만이 아니라 일반적으로 어떤 관계나 성질을 ‘보존’ 하는 함수 |
INTRODUCE PRODUCT
수학을 쉽고 의미있게 담아내는 수학교구 및 소프트웨어를 개발하여
수학문화의 대중화를 실천합니다.
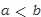 일 때, 양변에 같은 수를 더하면, 이런 것이 아니라, 양변에 같은 함수를
일 때, 양변에 같은 수를 더하면, 이런 것이 아니라, 양변에 같은 함수를


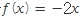 같은 경우만
같은 경우만 






