|
왜 교집합, 합집합이 중요한가?
작성자 : 수학사랑|조회수 : 7287 |
이 글은 저널 '수학사랑' 55호(2006년 3/4월호)에 실렸던 필자의 글을 조금 고친 것입니다.
따짐이: 선생님, 중학교하고 고등학교에서 집합을 배우죠? 선생님: 그렇지. 중학교 1학년(7-가 단계)에 간단히 나오고, 고등학교 1학년(10-가 단계)에서 좀 더 자세히 나오지. 따짐이: 그 단원에서 제일 핵심적인 용어를 찾는다면 무엇일까요? 선생님: 글쎄, 아마 교집합, 합집합이라는 용어가 아닐까? 따짐이: 바로 그거거든요. 제가 그 단원들 배우고 나서 생각해 보니까 결국 교집합, 합집합에 대한 얘기인 것 같아요. 선생님: 그런데? 따짐이: 그게 그렇게 중요한 내용인가요? 다른 곳에 별로 응용되는 것 같지도 않던데. 선생님: 그래도 도형의 교점이라든가, 연립방정식이나 연립부등식의 해 같은 것은 교집합을 가지고 일관성 있게 설명할 수 있지. 따짐이: 그건 그렇지만, 분배법칙이나 드모르간의 법칙같은 복잡한 내용까지 공부하는 것은 응용하고는 좀 거리가 있는 것 아닐까요? 선생님: 좀 그런 면이 있지. 따짐이: 그럼 왜 교집합, 합집합이라는 용어(개념)가 그렇게 중요하게 다루어지는지 말씀해 주시면 안 될까요? 선생님: 그것들이 연산(operation)이기 때문이라고 볼 수 있지. 따짐이: 연산? 사칙연산 같은? 선생님: 그렇지. 사칙연산은 수에 대한 연산이고, 교집합을 구하는 ∩ 따짐이: 저는 연산이란 말을 막연히 계산 같은 것이라고 생각하고 있었는데요. 선생님: 뭐, 교집합이나 합집합을 구하는 것도 계산이라고 볼 수도 있겠지. 집합 두 개로부터 새로운 집합을 구하는 일이니까. 따짐이: 선생님 말씀을 듣고 있다 보면 알고 있던 것도 헷갈려요. 선생님: 글쎄, 아마 정확하게 알고 있지 않았기 때문이겠지. 물론 그것은 네가 공부를 제대로 안 했다는 것이 아니야. 학교에서는 수학 개념들을 정확하게 알려주기 어려울 때가 많아서 그런 거지. 따짐이: 왜요? 선생님: 왜 정확하게 알려주기 어렵냐고? 따짐이: 예. 선생님: 그건 내가 항상 말했듯이, 하나의 수학 개념에 연결된 것들이 하도 많아서 배우는 과정에서는 정확히 말해 줄 수 없고 두루뭉술하게 넘어가야 할 때가 많기 때문이야. 일단 따로따로 배우고 나서 나중에 연결시켜 생각하는 것이지. 장님이 코끼리에 대해서 알려면 일단 다리, 코, 귀, 몸통, 꼬리를 따로따로 만져 보고 나중에 연결시켜 생각해야 하는 것과 마찬가지로. 그런데 물어 본 게 이거였나? 따짐이: 아니요. 왜 교집합, 합집합이라는 용어(개념)가 그렇게 중요하게 다루어지는지... 선생님: 그것들이 연산(operation)이기 때문이라고 볼... 따짐이: 그 말씀은 아까도 하셨고요, 연산이 무엇인지 정확히 잘 몰라서요. 선생님: 아 그렇지. 연산이란, 어떤 대상 두 개로부터 같은 종류의 새로운 대상 한 개를 만드는 과정이라고 보면 돼. 수학적으로는 하나의 연산은 그 자체가 하나의 함수로 정의되지만, 그건 나중에 생각해도 될 것 같고. 따짐이: 그러니까, 덧셈이나 곱셈은 두 개의 수로부터 하나의 수를 만들어내는 것이니까 수의 연산이고, 교집합이나 합집합은 두 개의 집합을 가지고 하나의 집합을 만들어내는 것이니까 집합의 연산이다 이거군요? 선생님: 그래, 바로 그렇지. 따짐이: 그런데 연산이면 다 중요한 것인가요? 선생님: 어떤 수학적 대상을 공부할 때 그것들 사이의 연산을 공부하는 것은 매우 중요한 일이야. 한정된 것에서 출발해서 계속 새로운 대상을 만들어갈 수 있는 방법이니까. 예를 들어 단원의 이름이 정수, 유리수, 실수, 복소수 등으로 되어 있어도 실제로 공부하는 것은 결국 그것들 사이의 연산이지 않니? 따짐이: 그런데 수학에서 배우는 대상은 수와 집합 말고도 많이 있잖아요? 예를 들어 함수, 도형 같은 것에는 연산이 없는 것 아닌가요? 선생님: 함수와 도형? 거기에도 다 연산이 있는데? 따짐이: 예? 선생님: 두 개의 함수를 가지고 새로운 함수를 만들 수 있지 않니? 따짐이: 음... 두 함수 f , g 가 있을 때 선생님: 그것도 그렇고, 고등학교 1학년(10-나 단계)에서 나오는 합성함수 같은 것은 바로 연산의 개념을 염두에 두고 나온 내용이야. 따짐이: 엇, 그러고 보니... 항등함수는 연산 ㅇ 의 항등원, 역함수는 역원에 해당하는 것이군요. 용어까지 비슷한데 몰랐네.
선생님: 도형에서 생각해 본다면, 점들을 대상으로 하는 연산으로 두 점의 x 좌표끼리 더하고 y 좌표끼리 더하는 연산이 있을 수 있지. 그럴 때는 점을 ‘벡터’ 라고 그럴싸하게 부르지만 결국 벡터는 점에다가 덧셈이라는 연산(그리고 스칼라배라는 다른 종류의 조작 - 이것도 ‘단항’ 연산이라 부르기도 함)을 할 수 있게 한 것에 불과해. 그뿐이냐? 두 개의 명제로부터 새로운 명제를 만드는 ‘그리고(AND)’, ‘또는(OR)’, ‘... 이면 ... 이다(→)’ 같은 것도 연산이지 않니? 따짐이: 그렇군요. 그러고 보니 연산들 사이에는 뭔가 통하는 점이 있는 것 같기도 해요. 각각의 연산들을 다른 용어를 써서 따로따로 배웠지만, 결합법칙 같은 것이라든지, 항등원, 역원 개념 같은 것... 어떤 수학적 대상들을 배우면서 그것들 사이의 연산에 주목하면 재미있겠네요. 서로 다른 대상들을 연산이라는 관점에서 일관성 있게 생각할 수도 있을 것 같고. 선생님: 아까도 말했듯이, 장님이 코끼리를 만져보듯이 어느 정도 이것저것 배우고 나면 그것들을 통합해서 생각하려는 노력을 해야 해. 기둥같이 생긴 다리와 뱀같이 생긴 코, 벽같이 생긴 몸통 등으로 따로따로 나누어져 있는 것으로 코끼리를 파악해서는 안 되지. 지금까지 배운 것을 돌아보면서 여러 단원을 꿰뚫는 통합적인 원리를 생각해 보는 것은 수학 공부를 할 때 꼭 필요한 자세라고 할 수 있어. |
INTRODUCE PRODUCT
수학을 쉽고 의미있게 담아내는 수학교구 및 소프트웨어를 개발하여
수학문화의 대중화를 실천합니다.
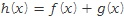 로 정의되는 함수... 뭐 이런 거요?
로 정의되는 함수... 뭐 이런 거요?






