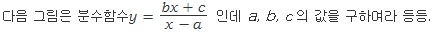|
어떻게 해야 수학 공부를 잘 할 수 있는가?
작성자 : 수학사랑|조회수 : 9219 |
| 이 글은 저널 '수학사랑' 54호(2006년 1/2월호)에 실렸던 필자의 글을 조금 고친 것입니다.
따짐이: 어떻게 하면 수학 공부를 잘 할 수 있을까요? 선생님: 음... 그건, 수학 공부를 잘 한다는 게 무슨 뜻이냐에 따라 대답이 달라지겠지. 따짐이: 글쎄요, 수학 공부를 잘 한다 못 한다를 구별하는 기준은 보통 수학 시험 점수이죠. 다시 말해 수학 공부를 잘 하는 방법이란, 수학 시험 점수를 올리는 방법을 말한다는 것이죠. 선생님: 수학 점수를 올리는 방법? 그것은 수학에서 배워야 할 것을 제대로 배우면 되지. 따짐이: 수학에서 배워야 할 것이 뭔데요? 선생님: 교과서에 나와 있는 지식들, 그리고 그것들 사이의 관계, 그리고 사물을 수학적으로 보는 사고방식, 그리고 수학이 가치 있다는 믿음, 이런 것들이지. 따짐이: 헐~ 선생님: 왜? 따짐이: 사람들은 보통 ‘교과서에 나와 있는 지식들’만 생각할 것 같은데요. 나머지 것들은 수학 점수를 올리는 데 소용이 없지 않을까요? 선생님: 그렇게 생각하기가 쉽지. 하지만 지식들 사이의 관계, 사물을 수학적으로 보는 사고방식, 수학이 가치 있다는 믿음 같은 것들은 비록 교과서에 명시적으로 나와 있지는 않고, 수학 시험에도 나오지는 않지만 수학 교육을 통해서 반드시 앞 세대에서 뒤 세대로 이어져야 하는 것이야. 수학은 서로 관계 지어지지 않은 단편적인 지식들의 집합이 결코 아니고, 수학을 가르치고 배우는 이유는 그런 단편적인 지식들을 전해 주는 것이 아니라는 거지. 따짐이: 하지만, 지금 방금 말씀하셨듯이, 그런 것들이 수학 교과서와 시험에 나오지 않는다면 수학 점수를 올리는 데 별 소용이 없지 않느냐는 것이죠. 선생님: 정말 그렇게 생각하니? 따짐이: 아니 뭐 꼭 그렇다기보다, 보통 그렇게들 생각할 것 같다는... 선생님: 눈에 보이는 결과에만 집착하면 정말 중요한 것을 놓치게 되지. 단기적으로는 복잡하게 생각할 것 없이 각 단원에서 시험 문제에 나올 수 있는 유형들을 나열하고 그것을 빠르고 정확히 풀 수 있도록 반복 숙달하는 것이 점수 올리기에는 도움이 될 수도 있어. 하지만 길게 보면 이야기가 달라지지. 따짐이: 왜요? 선생님: 시험문제에서 위력을 발휘하는 ‘문제풀이용 지식’들은 대개 해당 단원, 해당 유형 문제에만 적용되지. 따짐이: 문제집을 보면 그렇게 되어 있어요. 문제 유형에 따라 어떻게 풀어야 하는지가 나와 있죠. 선생님: 문제 유형별 풀이 방법을 익히고, 그것도 실수를 방지하기 위해 반복 숙달하다 보면, 그 사람의 정신에 자리 잡은 수학 지식이란 어떤 것이 될까? 수학적 지식이란 이리 저리 얽혀 있는 그물과 같은 것인데, 그 연결이 대부분 잘려 산산이 흩어진 상태로 그저 ‘쑤셔넣어져’ 있게 되지 않을까? 따짐이: 연결 그 자체를 만드는 데 시간과 노력이 든다면 그것이 효율적이겠죠. 선생님: 그래서 단기적으로는 점수 올리는 데 도움이 될 수 있다는 거지. 하지만, 그런 식으로 서로 연결되지 않은 지식의 집합을 언제까지 계속 담아 둘 수 있다고 생각하니? 따짐이: 모르죠. 하지만 수능 시험 볼 때까지만 넣어 두면 되니까... 선생님: 그래. 그렇게 생각하는 사람이 많지. 하지만 이렇게 단편적인 것들의 집합을 계속 기억하려면 점점 더 많은 반복 숙달이 필요해지지. 이것을 몇 년간 계속한다는 것은 매우 고통스러운 일이야. 따짐이: 그래서 수학 하면 몸서리치는 사람들이 많죠. 선생님: 그렇지. 수학은 그런 식으로 공부하기에는 가장 부적당한 과목이고, 내용도 엄청 많으니까. 어쨌든 그런 식으로 하다보면 이미 넣어져 있는 것이 많을수록 새로 무엇인가를 집어넣기는 점점 어려워지게 되겠지. 심리적인 압박감이 생김은 물론, 점수 올리기에도 실패할 가능성이 매우 높아. 또한, 예컨대 수능 시험을 보고 나면 반복 숙달을 계속하지 않을 테니 그런 지식은 급속도로 사라지고, 그 사람에게 고통스러웠던 기억만을 남기게 되겠지. 이것이 시험 점수 올리기식, 문제유형 반복 숙달식 공부의 한계야. 따짐이: 그렇다면 어떻게 해야 수학 공부를 잘 할 수 있을까요? 선생님: 제대로 공부해야지. 수학에서 배워야 할 것을 모두 배우면서. 따짐이: 예를 들어서 어떻게요? 선생님: 예를 들어, 중학교 때부터 여러 가지 함수를 배우지. 일차함수, 이차함수, 분수함수, 무리함수, 삼각함수, 지수함수, 로그함수 등등. 이런 것을 배울 때마다 반복 숙달해야 할 문제 유형이 늘어난다고 생각하면 얼마나 괴로울까? 따짐이: 그렇겠죠. ‘삼각함수 같은 건 누가 만들어서 나를 이렇게 고생을 시키는 거야!’ 이러면서. 선생님: 하지만 각 단원에서 우리가 하고 있는 것은 사실 똑같은 일이야. 식과 그래프의 관계를 탐구하는 일이지. 모두 같은 원리로 설명 가능하다는 이야기야. 예를 들어 각 함수 단원에는 모두 그래프가 어떤 특정한 점을 지난다는 조건을 사용하여 함수의 식에 들어 있는 미정계수를 구하는 문제가 있지. 직선 어떤 이차함수의 그래프의 꼭지점이 (1, 2)이고 (0, 3)을 지날 때 그 이차함수의 식을 구하여라, 이것들이 하나의 원리로부터 나온, 모두 연결되어 있는 문제라는 생각을 할 줄 아는 학생에게는 새로운 함수를 하나씩 공부해 간다는 것은 괴로운 일이 아니라 재미있는 일이고, 저금통장에 돈이 쌓여 가는 것처럼 뿌듯한 일이야.
따짐이: 맞아요. 하나의 원리로 여러 가지를 설명할 수 있다는 것을 깨달을 때나, 수학이 아닌 다른 곳에서 수학적 원리를 적용해서 문제를 해결할 수 있다는 것을 깨달을 때, 수학을 배운 보람이 있다고 생각하게 되더라고요. 선생님: 그래. 문제를 풀어 보는 것은 공부를 하기 위한 좋은 방법이야. 교과서에 문제들이 나와 있는 원래 이유는, 문제를 푸는 경험을 통해 ‘아, 맞아. 그래프는 그 식을 참으로 만드는 순서쌍 (x, y) 들의 집합이었지. 그러니까 그래프가 어떤 점을 지난다는 것은 그 점의 좌표가 식을 만족한다는 뜻이지’ 하는 식으로 함수와 그래프의 관계에 대한 원리를 확실히 이해하고, 그 원리가 어떻게 구체적인 상황에 적용되는지 깨닫는 것이야. 그렇게 원리를 이해한다면, 예를 들어 두 그래프의 교점의 좌표를 구하는 문제를 만났을 때, 전혀 그런 유형의 문제를 풀어 본 적이 없더라도 그 원리에 비추어서 생각하여 그 풀이 방법을 ‘발견’할 수 있겠지. 원리를 모르고 문제 풀이 방법만 연습했다면, 새로운 문제는 새로이 연습해야 할 또 하나의 대상일 뿐일 테고. 따짐이: 점수는 좋은데 못 보던 문제를 만나면 곧 포기하는 친구가 있는가 하면, 끝까지 문제를 붙잡고 마침내 풀이를 알아내는 친구도 있어요. 그런 차이군요. 선생님: 그런 식으로 큰 원리를 생각하면서 모든 것을 연결 지어 생각하면 12년간 배우는 수학 교과서의 내용도 결코 많은 것이 아니야. 몇 개의 원리로 모두 설명 가능하니까. 게다가 배우면 배울수록 서로서로 연결되어 더 많은 것을 배울 수 있는 실력(수학적 사고력, 문제 해결력)이 생기게 되지. 그렇게만 된다면 사물을 수학적인 원리에 비추어 볼 수 있는 안목도 저절로 생기고, 수학이 왜 가치 있는 학문인지 누가 말해 줄 필요도 없게 돼. 결국 시험 점수도 올라가게 되겠지. 점수를 올리기 위해 공부하는 것이 아니라 공부를 해서 그 결과로 점수가 올라가는 것, 이것이 제대로 공부했을 때 일어나는 일이야. 따짐이: 그렇게 수학을 ‘지대(제대로)’ 공부하는 학생이 몇이나 될까요? 선생님: 별로 없는 것 같아. 제대로 공부를 하려면 점수에 직접 관련이 없는 것이라도 충분히 고민하고 탐구해 보는 것이 필요한데 보통 그러지 않는다는 거야. 예를 들어 문제를 풀 때 그 풀이 방법이 어떻게 해서 나왔는지 기본 원리에서부터 차근차근 짚어 보지 않고 풀이 방법 그 자체만 알면 넘어가 버린다거나, 집합 단원에서 나오는 교집합과 일차 부등식에서 나오는 교집합, 부등식의 영역에서 나오는 교집합이 있다고 할 때 그것들이 왜 같은 개념이 되는지 따져보려고 하지 않고 각각의 단원에서 문제 풀이 방법만 계속 반복해 연습한다든지, 이런 식으로 공부를 한다는 거지. 이건 공부가 아니라 문제 풀이 훈련에 불과하다고 봐야 해. 따짐이: 왜 그렇게 되었을까요? 선생님: 당장의 점수에 초조해하고 조바심 내는 학생과 학부모도 문제지만 교육이 ‘상품’으로 취급되는 사회 환경이 사람들을 그렇게 만들었다고도 할 수 있지. 따짐이: 교육이 상품이면, 소비자인 학생이나 학부모의 필요에 맞는 교육이 되는 게 아니고요? 선생님: 그게 그렇게 간단한 문제는 아니야. 예를 들어 식품도 그래. 식품이 상품이니까 결국 어떻게 되었지? 제대로 된 식품보다는 당장 입에 당기고 보기 좋은 식품들이 넘쳐나지. 교육의 경우 학생이나 학부모의 ‘필요’ 라는 것은 사실 점수에 대한 조바심에 불과한 경우가 많아. 교육이라는 상품을 파는 쪽에서 자기들에게 유리한 방향으로 만들어 가고 있다고도 할 수 있고. 어쨌든 그 결과가 지금 보고 있는, 시험 점수 올리기식의 얕은 공부의 거대한 물결이라고 할 수 있지. 따짐이: 제대로 공부하려고 해도 사회가 안 도와준다... 선생님: 그래. 바로 그렇지. 이런 사회에서는 가정, 학교, 학원, 국가(정부) 등이 제대로 된 공부를 도와줄 거라고는 생각하지 않는 게 좋아. 스스로 의식을 갖고 정신을 바짝 차리는 수밖에 없지. |
INTRODUCE PRODUCT
수학을 쉽고 의미있게 담아내는 수학교구 및 소프트웨어를 개발하여
수학문화의 대중화를 실천합니다.
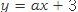 의 그래프가 점 (3, 0)을 지날 때 a 의 값을 구하여라,
의 그래프가 점 (3, 0)을 지날 때 a 의 값을 구하여라,