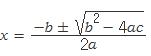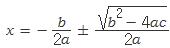|
이차방정식 근의 공식 다시보기
작성자 : 수학사랑|조회수 : 5170 |
1980년대 후반쯤 후배들의 교생 실습을 하고 있을 때의 일이다. 확실치는 않지만 모교 교수님들이 방문하여 고등학교 1학년 수업 참관 평가회를 하는 자리에서 나온 얘기이다... 왜 이차방정식의 근을 유도하고 다시 대입하여 확인하지 않느냐는 지적을 하셨다.
p⇒q, q⇒r, ...., ⇒w 와 같이 "...이면...이다"로 이어진 과정에서 얻어진 결론이 반드시 처음 조건 p를 만족한다는 보장이 없기 때문에 대입하여 확인하는 과정을 학생들에게 강조해야 한다는 것이다.
공식을 외우고 문제를 푸는 것에 익숙했던 학습 환경에서 간과했던 내용으로 오래동안 마음에 남아 있었지만 실제로 적용해 볼 기회가 적었다. 공고에 있을 때 한 번 시도해 보았는 데 근의 공식을 대입하여 계산하는 과정에서 학생들이 외면하였다. 또 2년전 경기고에 처음와서 시도해 보았는 데 아이들은 눈을 동그랗게 뜨고 나를 이상하다는 듯 쳐다 보았다. 그런데 정작 나는 근의 공식을 대입하여 계산한 것이 0 이 될 때 참 기분이 좋다는 느낌을 받았다. 그뿐아니라 이 계산을 한 번 해본 학생들은 근의 뜻을 누구보다도 확실하게 체험적으로 깨닫을 수 있다는 믿음이 생겼다. 복잡한 공식이 대입되어 도저히 0 이 될것 같지 않은 데... 이래서 수학이 신기하고 재미있는 것이 아닐까? 우리 학생들도 반드시 이런 기분을 느낄 수 있도록 또 다시 시도해 볼 작정이다. 물론 시나리오를 잘 짜야한다...
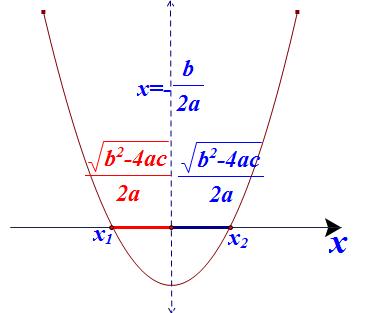
이차방정식 이것을 다음과 같이 고쳐써보고 그 의미를 생각해 보자.
즉, 근의 공식 속에 대칭축의 방정식이 숨어 있는 것이다.
한편 이차함수의 대칭축은 y축 평행이동에 영향을 받지 않으므로
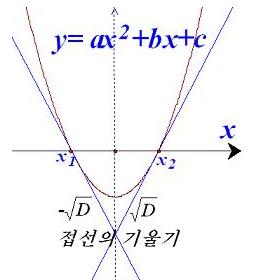
다음에는 얼마전 NCTM 잡지에서 본 것을 소개한다.
|
INTRODUCE PRODUCT
수학을 쉽고 의미있게 담아내는 수학교구 및 소프트웨어를 개발하여
수학문화의 대중화를 실천합니다.
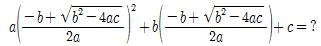
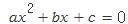 의 근은 다음과 같다.
의 근은 다음과 같다.